如何从数据中提取特征?
| 传统机器学习 | 深度学习 |
|---|---|
| 手工提取特征 | 自动学习特征 |
| 非端到端 | 端到端 |
特征是什么?
- 关键信息
特征的性质?
-
最好对缩放、旋转等变换鲁棒
=> 数据增广 (data augmentation):对同一张图片进行不同比例缩放、不同角度旋转,加入数据集
=> 维数爆炸
数据预处理的方法
$L_p$归一化 ($L_p$ Normalization)
$L_p$范数:$(\sum_i \mid x_i \mid^p)^{\frac{1}{p}}$
$L_p$归一化:$\tilde{x} = \frac{x}{(\sum_i \mid x_i \mid^p)^{\frac{1}{p}}}$
在$L_p$归一化后,$\tilde{x}$的$L_p$范数是1
现有二维特征$\tilde{x} = [\tilde{x}_1, \tilde{x}_2]$,且$(\mid \tilde{x}_1 \mid^p+\mid \tilde{x}_2 \mid^p)^{\frac{1}{p}}=1$,下图展示了$\tilde{x}_1$和$\tilde{x}_2$的关系:
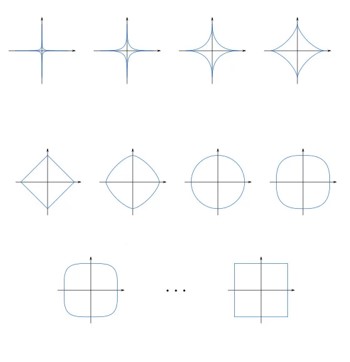
Z-Score归一化
对于二维特征$x=[x_1,x_2]$,令$\tilde{x} = [\tilde{x}_1, \tilde{x}_2]$,其中$\tilde{x}_1=\frac{x_1-\mu_1}{\sigma_1}$,$\tilde{x}_2=\frac{x_2-\mu_2}{\sigma_2}$


空间金字塔 (Spatial Pyramid)
将同一张图片依次分成16块、4块、1块,然后再把这些块连起来,得到的新特征能够保留图片的空间信息
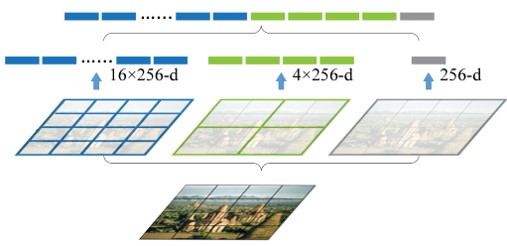
(虽然这样会大大增加特征的维数,降维方法将在下一章介绍)