Dimensionality Reduction

1. 高维诅咒 Curse of Dimensionality

对于一个640*640的RGB图片来说，如果保留所有的像素，向量长度将达到640*640*3=1,228,800维。如果是视频，乘上帧率和时长，维数将变得更高。

这就引发了高维诅咒的问题：

高维诅咒对时间和空间复杂度提出了很高的要求。存储的成本和耗时都将增加。
对于同样数量的样本，在更高维度空间中就会变得稀疏，所以高维空间需要更多训练样本来填充整个空间。从另一个角度来说，这也会增加模型的复杂度，导致过拟合（模型复杂度、训练样本少）的风险。

高维物体的体积集中在表面：

\[\lim_{d\rightarrow\infty} \frac{V_d(1-\epsilon)}{V_d(1)} = \lim_{d\rightarrow\infty}(1-\epsilon)^d=0\]

对于两个均服从在$[0,1]^d$上均匀分布的变量x和y，它们之间的距离$\parallel x-y \parallel ^2$满足$E[\parallel x-y\parallel ^2]=\sqrt{\frac{d}{6}}$。

维度越高，距离的期望越高，方差却越小。直观上来说，就是样本都聚集在一起，这对于按距离进行分类的分类器（比如KNN）来说很不友好。

2. 降维 Dimensionality Reduction

降维的motivation：

降低时间和空间的复杂度
去除冗余信息和噪声
避免高维诅咒

降维可以分为三类：

特征选择 Feature Selection
特征投影 Feature Projection
特征学习 Feature Learning

实际上，特征选择也可以视作特征投影的一种特殊情况，所以也可以说分成特征投影和学习两大类。

3. 特征选择 Feature Selection

特征选择有三大类方法：

过滤式 Filter Methods
包裹式 Wrapper Methods
嵌入式 Embedded Methods

过滤式

过滤式给每个特征打分，按分数高低排名，可以按threshold筛选，也可以选取前k个。

卡方检验Chi Squared Test是一种很典型的过滤式方法。

\[\sum_{i=1}^n \frac{(f_i-E)^2}{E}\]

上面这个式子就是卡方检验的衡量公式。f是实际值，E是理论值，将样本$f_1, f_2, …, f_n$代入上面的式子计算卡方值。

我们的原假设是特征f与类别C无关，因此卡方值越大，偏离原假设的程度越大，也就是说卡方值越大f与C越相关。计算了卡方值就可以按照设定的阈值对f进行筛选。

另一种常用的过滤式方法是信息增益 Information Gain:

\[IG(X, Z) = H(X) - H(X \mid Z) = H(Z) - H(Z \mid X)\]

信息增益也叫互信息 Mutual Information，满足交换律和非负性。

此外，容易推导信息增益和KL散度的关系

\[IG(X, Z) = KL(p(x, z) \parallel p(x)p(z))\]

我们可以计算$IG(f, C)$，它表示了包含或不包含特征f时，为分类器C的识别能提供多少信息量。

除了以上介绍的卡方检测和信息增益，在作业中我们实际使用了另一种方法，就是计算每个特征的方差来进行筛选。这种方法基于这样的思想：如果大多数样本在某一特征f上都取同一个值，这个特征就比较鸡肋，不要也罢。所以可以计算每个特征f的方差，低于某个阈值就去除。一般将阈值设为$0.8*(1-0.8)$。

包裹式

包裹式将特征选择的过程视为一个搜索问题。评价函数能够给每种特征组合进行打分，目标是找到打分高的特征子集。

课程中提到的前向和后向搜索都属于包裹式的方法。当然，前向和后向搜索本身都不是一种方法，而是一类方法，可以用不同的判定标准来决定是否保留或去除特征。

嵌入式

嵌入式在创建模型的同时选择对模型分类准确率最有帮助的那些特征，常见类型是正则化方法，例如LASSO、Elastic Net和岭回归 Ridge Regression。

假设样本都去中心化了，即$\sum_{i=1}^nx_i=0$，线性回归的优化目标就可以记作

\[\beta^* = \arg\,\min_\beta \frac{1}{n} \sum_{i=0}^n (y_i-\beta^Tx_i)\]

这里的$\beta$不包含偏置项。

为了使模型不那么复杂，需要对$\beta$的模进行限制，LASSO和岭回归的区别就在于正则项使用L1还是L2范数：

LASSO的优化目标是

\[\beta^* = \arg\,\min_\beta \frac{1}{n} \parallel y-X\beta\parallel^2_2 + \lambda \parallel \beta\parallel_1\]

岭回归的优化目标是

\[\beta^* = \arg\,\min_\beta \frac{1}{n} \parallel y-X\beta\parallel^2_2 + \lambda \parallel\beta\parallel_2^2\]

那如何使用LASSO和岭回归进行特征选择呢？很简单，$\beta^*$里的元素越大，对应的特征权重越大，依此选择特征即可。

4. 特征投影 Feature Projection

分为线性投影和非线性投影。

线性投影可以表示为$f’=Pf$，着重介绍PCA和LDA
非线性投影可以表示为$f’=p(f)$，着重介绍Kernel PCA和自动编码器 Auto-encoder

PCA

PCA的思想是将高维映射到相互正交的k维上。

有两种等价的形式化表述：

max 投射后向量长度的方差（当X去中心化时）

\[\frac{1}{n}\sum_{i=1}^n (v^Tx_i)^2 = \frac{1}{n} v^TXX^Tv\]

min 重建误差

\[\frac{1}{n}\sum_{i=1}^n \parallel X_i-(v^Tx_i)v\parallel^2\]

由于两种表述等价，这里只推导第一种。

抽象成优化问题

\[\max_v \quad v^TXX^Tv \\ s.t.\quad v^Tv = 1\]

Lagrange multiplier:

\[\mathcal L_v = v^TXX^Tv + \lambda(1-v^Tv) \\ \frac{\partial \mathcal L_v}{\partial v} = 2XX^Tv - 2\lambda v = 0 \\ XX^Tv = \lambda v\]

所以$\lambda$是矩阵$XX^T$的特征值，v是特征向量。

降维取多少维，是按照特征值从大到小取前多少个特征向量。例如要降到N维，就取最大的N个特征值对应的特征向量。

Kernel PCA

将上面推导的式子中$X$换成$\phi(X)$，$v$换成$\phi(X)\alpha$：

\[\begin{aligned} &\qquad XX^Tv = \lambda v \\ &\Rightarrow \phi(X)\phi(X)^T\phi(X)\alpha = \lambda\phi(X)\alpha \\ &\Rightarrow \phi(X)^T\phi(X)\phi(X)^T\phi(X)\alpha = \lambda\phi(X)^T\phi(X)\alpha \\ &\Rightarrow KK\alpha = \lambda K \alpha \\ &\Rightarrow K\alpha = \lambda \alpha \end{aligned}\]

其中$K = \phi(X)^T \phi(X)$

LDA

LDA的思想是找一个方向，使得在这个方向上类间的间距最大，同时类内的间距又较小，从而能够方便地区分不同类别。

\[\begin{aligned} J(v) &= \frac{(v^T\mu_1-v^T\mu_2)^2}{\sigma_1^2+\sigma_2^2} \\ &= \frac{(v^T\mu_1-v^T\mu_2)^2}{\sum_{i=1}^{C_1}(v^Tx_{1,i}-v^T\mu_1)^2+\sum_{i=1}^{C_2}(v^Tx_{2,i}-v^T\mu_2)^2} \\ &= \frac{v^T(\mu_1-\mu_2)(\mu_1-\mu_2)^Tv}{v^T[\sum_{i=1}^{C_1}(x_{1,i}-\mu_1)(x_{1,i}-\mu_1)^T+\sum_{i=1}^{C_2}(x_{2,i}-\mu_2)(x_{2,i}-\mu_2)^T]v} \\ &= \frac{v^TS_Bv}{v^TS_Wv} \end{aligned}\]

虽然$v$的长度可以任意变化，但是我们并不关心它，所以可以假设$v^TS_Wv=1$，就转化成以下优化问题：

\[max_v \quad v^TS_Bv \\ s.t. \quad v^TS_Wv = 1\]

Lagrange multiplier:

\[\begin{aligned} &\qquad \mathcal L_v = v^TS_Bv - \lambda(v^TS_Wv-1) \\ &\Rightarrow \frac{\partial \mathcal L_v}{\partial v} = 2S_B v - 2\lambda S_Wv = 0 \\ &\Rightarrow S_Bv = \lambda S_W v \\ &\Rightarrow S_W^{-1} S_B v = \lambda v \end{aligned}\]

因此，$v$是矩阵$S_W^{-1}S_B$的特征向量。

自动编码器 Auto-Encoder

自动编码器是一种无监督学习，通过让重构数据逼近原始数据，不需要手工标注的数据就可以完成训练。

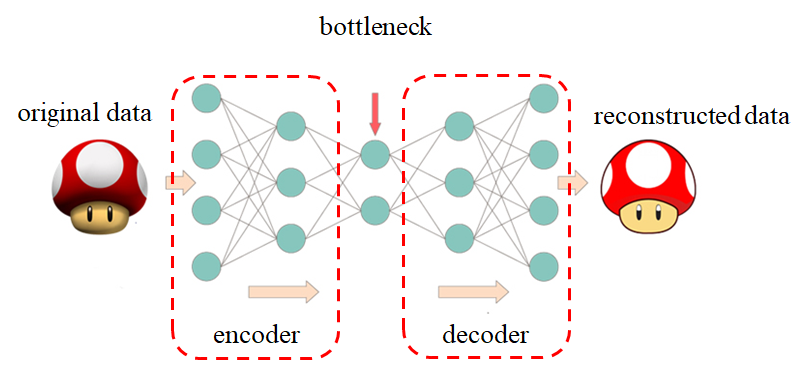
如图所示，自动编码器由编码器、bottleneck和解码器三部分组成。bottleneck就是我们所需要的低维特征（图示中是漏斗形的，可获得低维特征，也有少数自动编码器的bottleneck比原始数据维数更高，可以增加数据的维数）。训练完成后，我们不需要解码器，将数据输入编码器就可以输出低维特征。

变分编码器 VAE (Variational Auto-Encoder)

下图展示了普通的自动编码器和VAE的区别

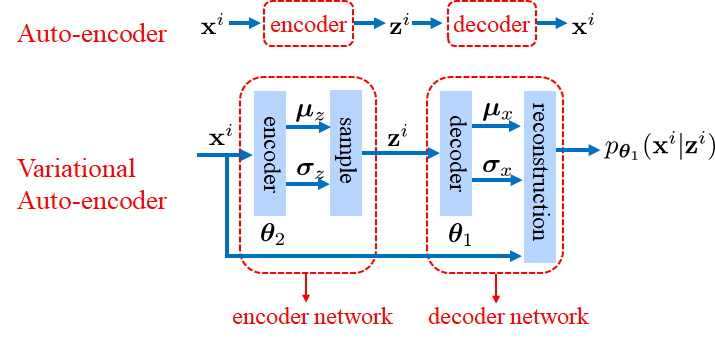
VAE的编码器和解码器学到的并不是向量，而是概率分布。例如编码器网络中，学到的是期望为$\mu_z$，方差为$\sigma_z$的一个高斯分布，并从中采样出$z^i$，解码器网络同理。

VAE最终的优化目标是

\[min_{\theta_1, \theta_2}\quad KL[q_{\theta_2}(z \mid x^i) \parallel p(z)] - \log p_{\theta_1}(x^i \mid z^i)\]

其中KL散度是控制$z$的误差，log是重构x的误差。

5. 特征学习 Feature Learning

要特别注意特征学习和之前提到的特征投影的区别，特征学习是直接学习降维后的特征，特征投影则是学习投影矩阵或者投影的函数

SNE (Stochastic Neighborhood Embedding)

思想：从$x$中学习到$\tilde{x}$，使得$\tilde{x}$能够保持$x$的相对距离（这里距离用高斯分布表示）

\[p(j \mid i) = \frac{exp(- \parallel x_i - x_j \parallel^2)}{\sum_{k\neq i}exp(- \parallel x_i - x_k \parallel^2)}\] \[q(j \mid i) = \frac{exp(- \parallel \tilde{x}_i - \tilde{x}_j \parallel^2)}{\sum_{k\neq i}exp(- \parallel \tilde{x}_i - \tilde{x}_k \parallel^2)}\]

$p(j \mid i)$和$q(j \mid i)$应尽量接近，所以目标是最小化KL散度：

\[L = \sum_i KL(P_i \parallel Q_i) = \sum_i \sum_j p(j \mid i) \log \frac{p(j \mid i)}{q(j \mid i)}\]

t-SNE是SNE的变形，区别在于使用的距离度量方式不是高斯而是（自由度为1的）t分布

\[p(j \mid i) = \frac{(1+\parallel x_i - x_j \parallel ^2)^{-1}}{\sum_{k\neq i}(1+\parallel x_i - x_k \parallel ^2)^{-1}}\] \[q(j \mid i) = \frac{(1+\parallel \tilde{x}_i - \tilde{x}_j \parallel ^2)^{-1}}{\sum_{k\neq i}(1+\parallel \tilde{x}_i - \tilde{x}_k \parallel ^2)^{-1}}\]

下图可以直观地看到高斯分布和t分布的区别：

高斯分布集中在平均值附近，边缘处的概率较小；t分布平均值处的概率略低，对边缘鲁棒性更高

LLE (Local Linear Embedding)

LLE是通过每个样本最近的K个点重建距离

LLE可以分为三个步骤：

找到每个样本$x_i$的K邻近点（不包含它自身）
解出重建权重矩阵$W$，具体步骤是：

对于每个样本$x_i$：
1. 创建矩阵$Z$，每一列是$x_i$的一个邻近点，总共K列
2. 从$Z$的每一列中减去$x_i$
3. 计算局部协方差矩阵$C=Z^TZ$
4. 从线性方程$C\cdot w=1$中解出行向量$w$（方程右边的$1$是一个全1列向量）
5. 如果$j$不是$i$的邻居，将$W_{ij}$设为0
6. $W$的第$i$行的其他元素：$\frac{w}{sum(w)}$
用权重矩阵$W$计算嵌入坐标$Y$(不知道怎么翻译比较好，原文是embedding coordinates)
1. 创建稀疏矩阵$M=(I-W)^T \cdot (I-W)$
2. 找到$M$的最后$d+1$个特征向量（这里指的是最小的$d+1$个特征值对应的特征向量）
3. 将$Y$的第$q$行（注意是行不是列）设为最小的第$q+1$个特征向量（因为最小的那个特征向量是全1向量，对应特征值0）

MDS (Multi Dimensional Scaling)

记样本$x_i = [x_{i1}; x_{i2}; … ; x_{ik}]$

记$B = X^TX$，即

\[\begin{aligned} d_{ij}^2 &= \parallel x_i - x_j \parallel^2 \\ &= x_i^Tx_i + x_j^Tx_j - 2x_i^Tx_j \\ &= b_{ii} + b_{ij} - 2b_{ij} \end{aligned}\]

若所有样本都去中心化了（这里是说每个样本的所有维，不是所有样本），则矩阵$B$的每一行和都是0：

\[\begin{aligned} &\quad \sum_{i=1}^n x_{ik} = 0 \\ &\Rightarrow \sum_{i=1}^n b_{ij} = \sum_{i=1}^n \sum_{k=1}^d x_{ik} x_{jk} = \sum_{k=1}^d x_{jk} \sum_{i=1}^n x_{ik} = 0 \end{aligned}\]

由以上两个式子可以推出：

\[\sum_{i=1}^n d_{ij}^2 = \sum_{i=1}^n b_{ii} + nb_{jj}\] \[\sum_{j=1}^n d_{ij}^2 = \sum_{i=1}^n b_{ii} + nb_{ii}\] \[\sum_{i=1}^n \sum_{j=1}^n d_{ij}^2 = 2n\sum_{i=1}^n b_{ii}\]

进而

\[b_{ij} = -\frac{1}{2} (d_{ij}^2 - \frac{1}{n}\sum_{i=1}^n d_{ij}^2 - \frac{1}{n} \sum_{j=1}^n d_{ij}^2 + \frac{1}{n^2} \sum_{i=1}^n \sum_{j=1}^n d_{ij}^2)\]

可以写成矩阵形式

\[B=-\frac{1}{2} H \overline{D} H\]

其中$\overline{D}_{ij} = d_{ij}^2$，且$H=I-\frac{1}{n}11^T$（$H$没有实际的物理意义，只是为了凑形式）

所以，给定距离矩阵$\overline{D}$，我们就可以计算出$B$（通过$B=-\frac{1}{2} H \overline{D} H$），然后根据$B = X^TX$就可以计算出$X$

下图是一个通过MDS展开瑞士卷的例子

首先是构造K近邻图$G$；然后对于 $G$中的每对点，计算最近的距离（也就是几何距离）；最后对集合距离矩阵使用MDS