之前介绍过特征的预处理方法(比如$L_p$ nomalization和Z-score),这次介绍对raw data的预处理方法。
数据平滑
中值滤波 (Median Filter)
用一个滑动窗口滑动向量/矩阵(或者说tensor),对窗口内的数计算中位数。
为了让新的tensor尺寸和原来的一样,可以用padding的方法增加边缘。

均值滤波 (Mean Filter)
均值滤波和中值滤波很相似,只是均值滤波用的是平均值,中值滤波是中位数。
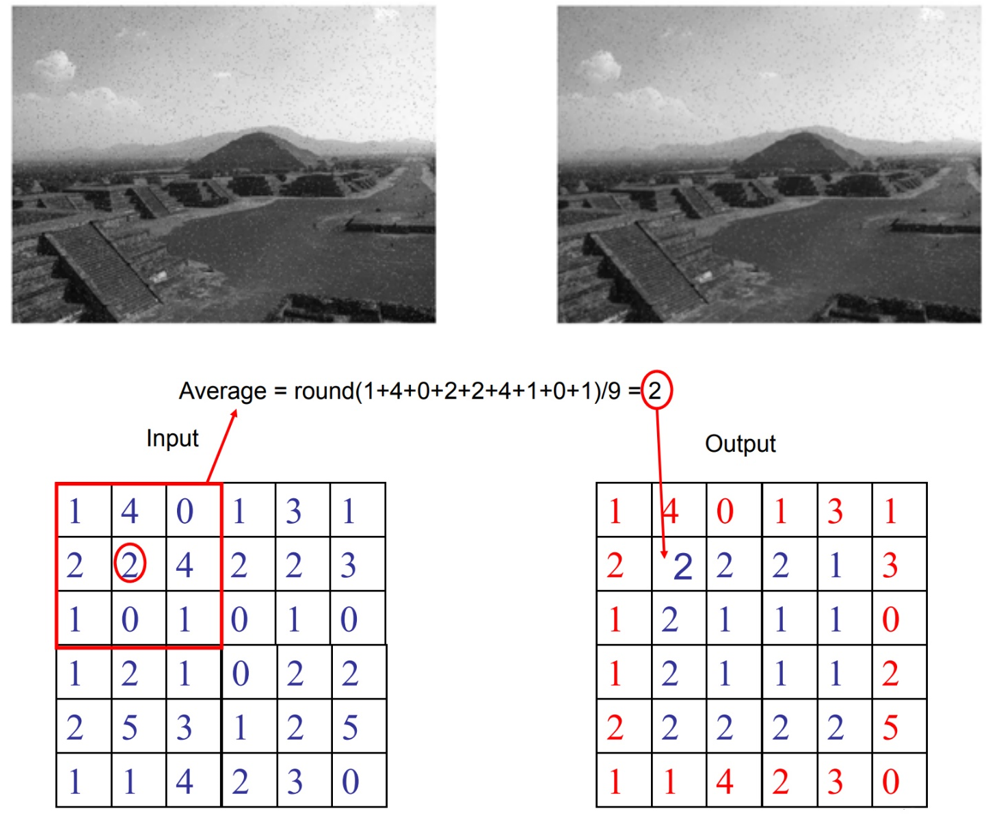
中值滤波和均值滤波的比较
从之前的图中可以看到中值滤波中的噪点数量少于均值滤波。这两种滤波方法的优缺点是什么呢?
| Median Filter | Mean Filter | |
|---|---|---|
| Pros | 能保留边缘的锐利;对离群点不敏感 | 快;平滑 |
| Cons | 慢;不平滑 | 边缘模糊,对离群点敏感 |
在计算速度方面,应注意到滑动窗口是一种增量计算的方法。当已知一个滑动窗口的平均值时,右移一格的新平均值很方便计算(加上右边一列,再减去左边那列),但中位数就不是这样了。
去除离群点 (Outliers)
统计的方法 (Statistical Methods)
先假设样本是高斯分布(或者其他分布也可以)的,拟合数据,去除离群点
用两个模型分别拟合离群点和非离群点。如果新来的点更接近于离群点的分布,那这个点就算作离群点
基于距离的方法 (Distance Based Methods)
邻近点的数量较少,即邻近点密度太低,就是离群点
如果某个点离它最近的邻居都很远,那就是离群点
基于学习的方法 (Learning Based Methods)
聚类,认为最小的那个类里面都是离群点
单类分类器(例如单类SVM)。这个可能比较难理解。在二分类器中,我们学习一个超平面,把正负样本分开。单类分类器中,我们学习一个分类器把数据包住,不能包住的就是离群点。
预先知道一些离群点和非离群点,训练一个二分类器(朴素贝叶斯、加权SVM二分类器都可以)。这里面可能会遇到数据量不均衡的问题,离群点的数量远低于非离群点。这时我们可以对离群点增加权重,让分类器对它们更加重视。
填充缺失数据
-
用平均值填充
-
回归现有的值对缺失数据进行估计
数据量子化
二值化 (Binarization)
将连续的值映射到两个值(就是2个bin)(比如将一张原始黑白照片变换为只有黑白二色的照片)

量子化 (Quantization)
将连续的值映射到多个(超过2个)bin(比如将正弦函数近似为锯齿状)
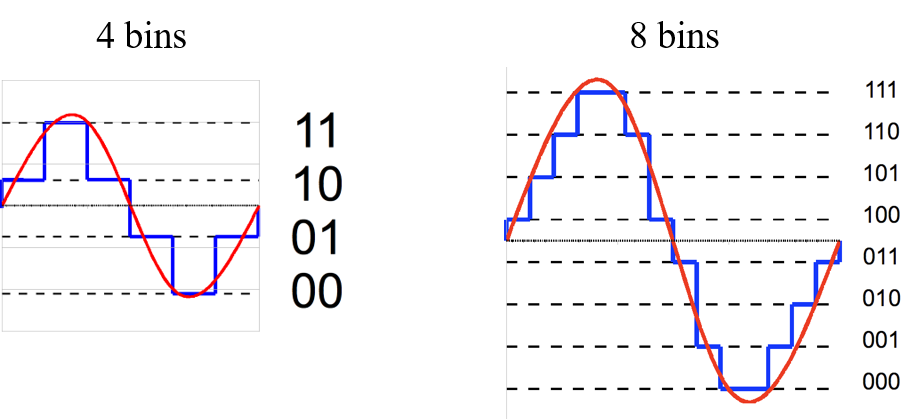
Tradeoff: bin的数量越少,存储空间越小,但丢掉的信息越多

基于聚类的量子化
从另一个角度看量子化,假设有$n$个样本$x_1, x_2, …, x_n$,每个样本都是$d$维特征$x_i=[x_{i, 1}, x_{i, 2}, …, x_{i, d}]$。
对这$n$个样本做聚类,假设有一个大小为$k$的密码本(codebook),就是说聚类将样本分成$k$类,每个类的聚类中心是$c_i$。
用距离样本最近的聚类中心对该样本进行编码,则编码长度$L=\log_2 k$(比特)。
以上这种方法是将每个样本看作一个整体,也可以将每个样本切成$m$段,每段长度为$d_0$。对每一段独立做量子化,每一段可以有不同的codebook。
则有
\[\begin{aligned} &d = d_0 \times m \\ &L = \log_2 k \times m \end{aligned}\]固定$d$和$k$,增大$m$,也就是减小$d_0$,分段的粒度就变细,保留的信息越多,代价是存储空间的增大。