看到一堆数字,或许很难发现其中的规律。但如果制作成图表,就能直观地发现其中的规律。
散点图 (Scatter Plot)
将很多小朋友的身高体重数据在图上戳点点,就可以得到散点图
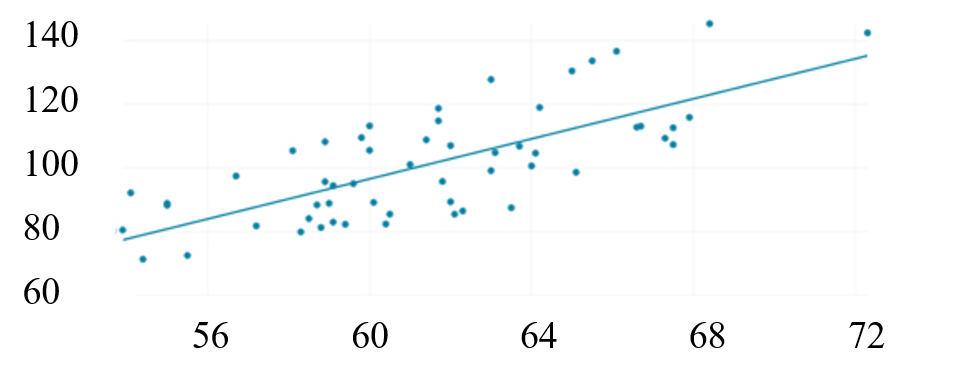
散点图一般可以用来做一些相关性的分析,比如从上图可以看出小朋友的身高体重是正相关的。
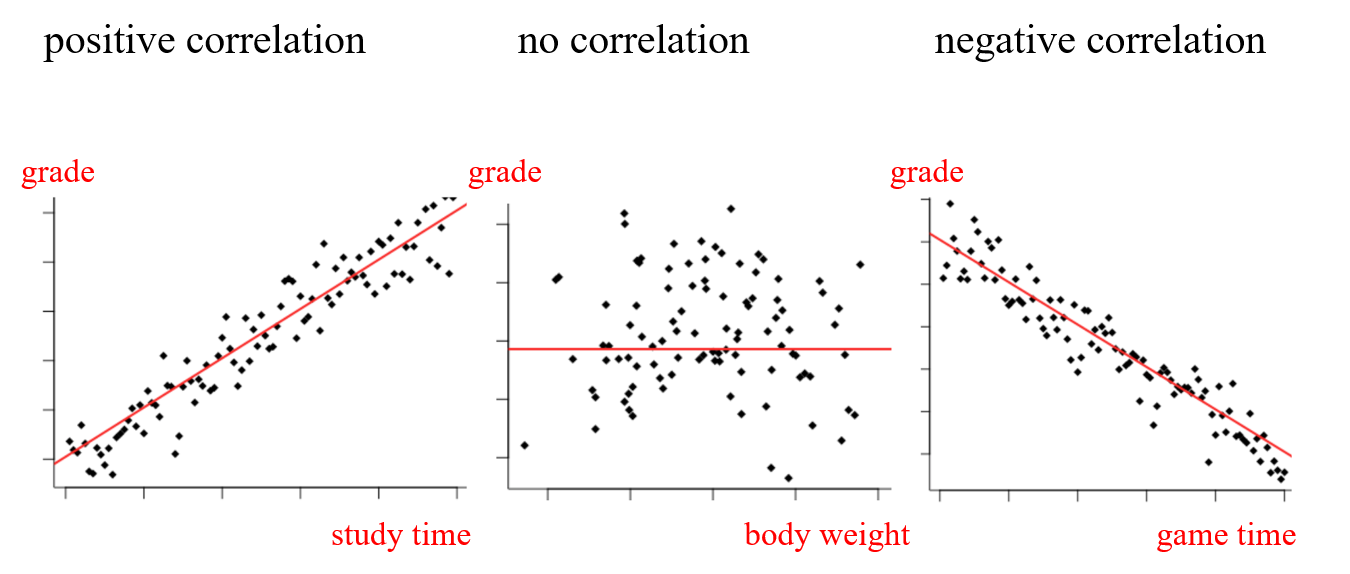
线形图 (Line Graph)
从图中能直观地看到比特币的价格随时间的变化:
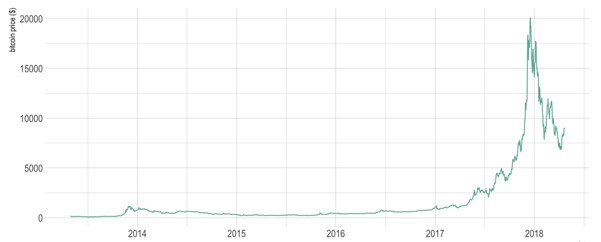
图表 (Chart)
柱状图 (Bar Chart)
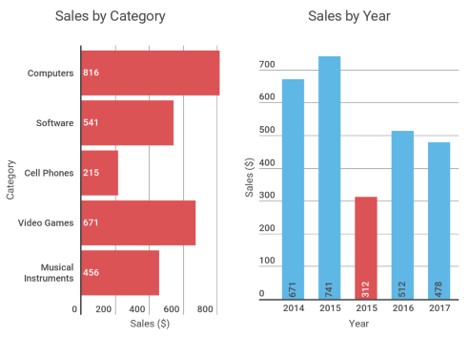
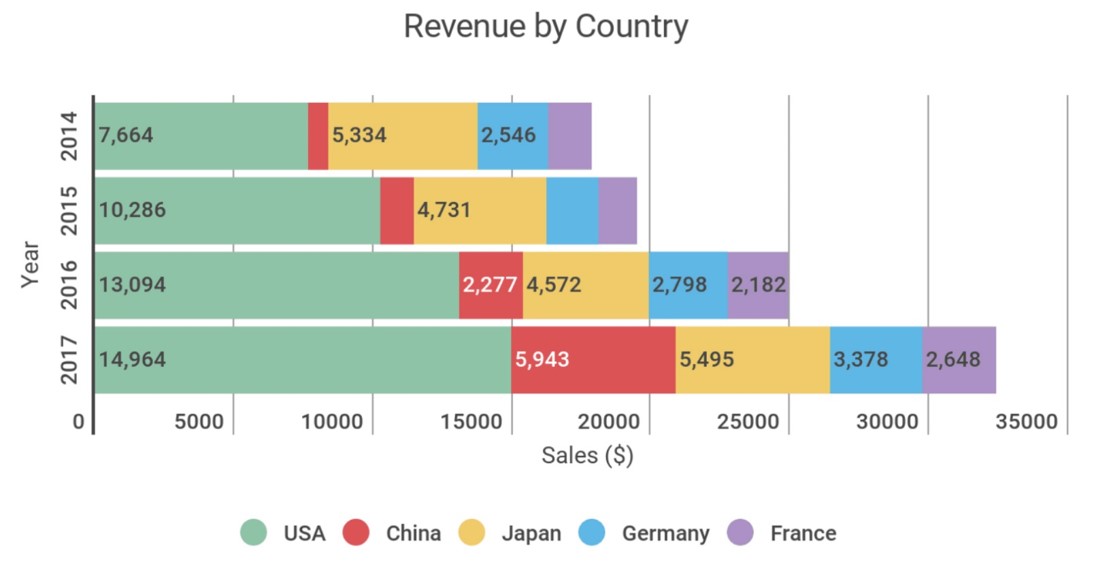
堆叠柱状图 (Stacked Bar Chart)
这种(fancy的)柱状图能比普通的柱状图反映更多的信息。例如在下图中,不仅能看到每年的财政收入,还能反映每年每个国家的财政收入,便于进行比较。
圆形的图表
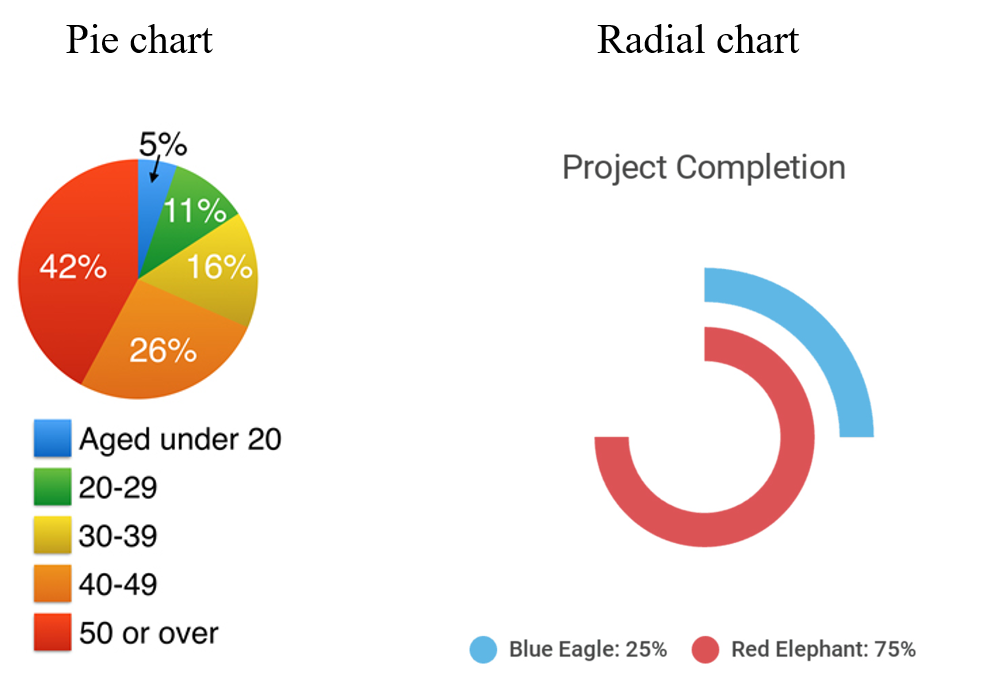
这里老师的比喻比较搞笑,饼状图就好比是一张披萨,反映了你吃了多少。而那个弧形的图表就好像是跑道,跑道有共同的起点,反映了每个运动员跑了多少圈。
不过右边那种弧形的图表现在不是很常用了。
箱型图 (Box Plot)
箱型图是一种比较美观,数据量也比较大的图表形式。
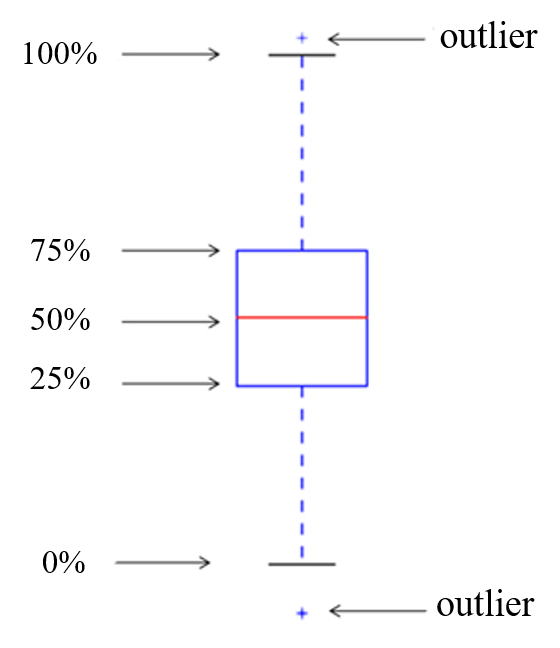
箱子的顶部和底部不一定是75%和25%,但默认是这样的。(老师比喻这个箱子长得像针筒,也是很形象了)
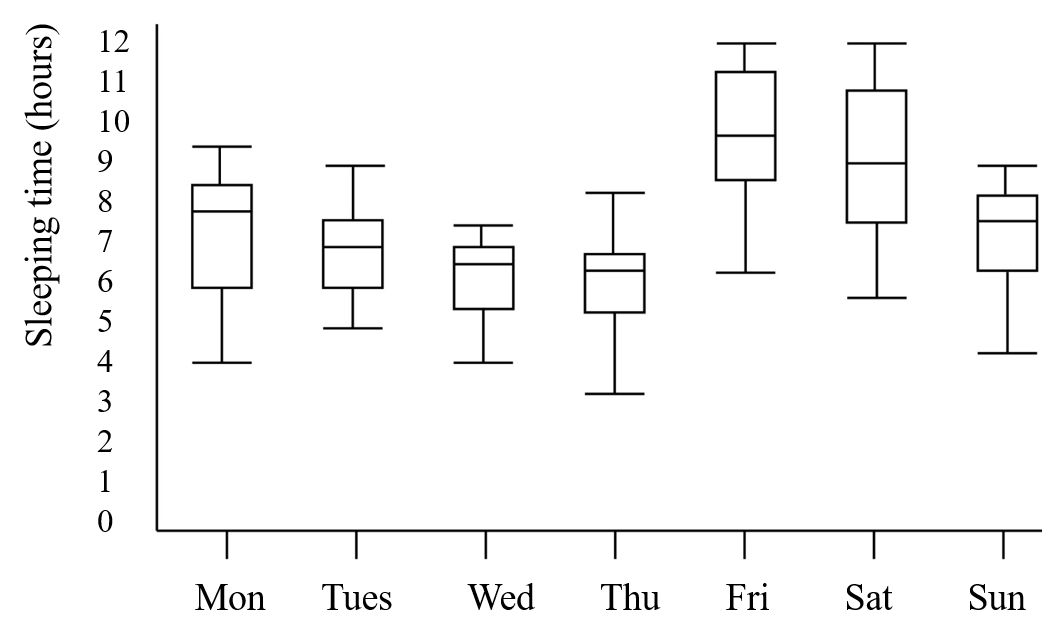
这是很多箱型图画在一张图里的效果。
高维图表
3D可视化
3D的图表比二维多一维,反映的信息更多一点。但总体而言只是二维的扩展而已。
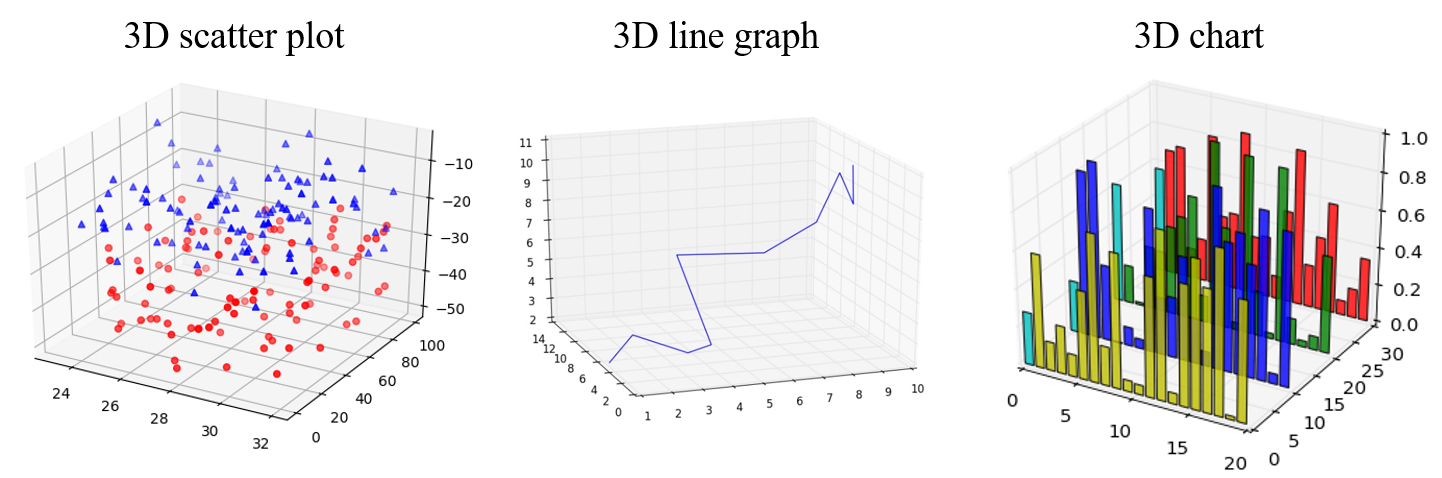
3D以上
三维以上就比较难可视化了,即便画出来,一般人也很难想象,所以需要对高维特征进行降维(进来复习数据降维)
降到多少维合适呢?
之前介绍数据降维的方式的时候,这取决于最后的任务。为了维持最后任务的性能,可能需要保留百分之八十或者九十的数据的能量。
但在可视化的过程中,降到多少维是由可视化的方便程度决定的,比如之前提到的,人最多能想象二维到三维的图。
t-SNE之前在数据降维的部分介绍过,但其实它在可视化方面也很重要。用t-SNE将数据降到二维就能方便可视化。如果一个特征学得足够好,两种样本在图上应该是分得足够开的。(下图是个反例)
